Direction Of A Vector Calculator

The Management Of A Vector – Explanation and Examples

In the realm of vector geometry, the direction of a vector plays a cardinal role. The direction of a vector is defined equally:

"The direction of a vector is the direction forth which it acts."

Keeping the importance of management in mind, let's movement forward.

We will be covering the following topics in this department:

What is the direction of a vector?
How to find the management of a vector?
What is the formula for finding the direction of a vector?
Examples
Practice bug

What Is The Management Of A Vector?

A vector is a physical quantity described by a magnitude and direction. A vector quantity is represented past a vector diagram and hence has a direction—the orientation at which the vector points is specified as the direction of a vector.

In convention, where its vector diagram represents a vector, its direction is determined by the counterclockwise angle it makes with the positive 10-axis. Co-ordinate to a calibration, the vector diagram is a line with an arrowhead that denotes the direction of the vector.

A = |A| Â

|A| represents magnitude, and Â represents the unit vector.

For example, to depict a torso'south velocity completely, we will have to mention its magnitude and management. This means that we volition have to mention how fast it is going in terms of altitude covered per unit time and describe what direction it is headed.

So, if we say a machine is moving at 40 km/hr. This statement just describes the speed of the body. If someone says a car is moving at forty km/hr and is headed North. This statement is describing the velocity of the motorcar. It tells u.s.a. the magnitude past which the car is moving and the direction in which it is headed.

This is why, for us to draw a vector, the direction is only as vital and the magnitude. If we were to say that the chocolates are 3 meters exterior of the classroom towards the North, it would make more than sense.

We have seen in the above-mentioned example how the direction is important to a vector quantity.

The arrowhead donates the direction of the vector, and the tail represents the point of activity. In that location are two conventional means to describe the direction of a vector.

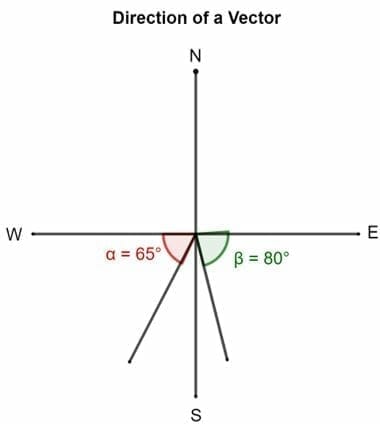
A vector's direction can be described by the angle its tail forms with East, North, West, or South. For instance, while describing a vector, it tin be said that a vector is directed eighty° S of Due east. This means that the vector has been rotated 80° from the Due east towards the Southward. The purple vector represents this.

Similarly, some other vector tin can be 65° South of the Due west. This ways that it is directed 65° about the tail from the W toward the South. The green vector denotes this.

Some other way to depict a vector is past the counterclockwise angle of rotation from the due "Eastward." According to this, a vector with a direction of 50° is directed fifty° from the East.

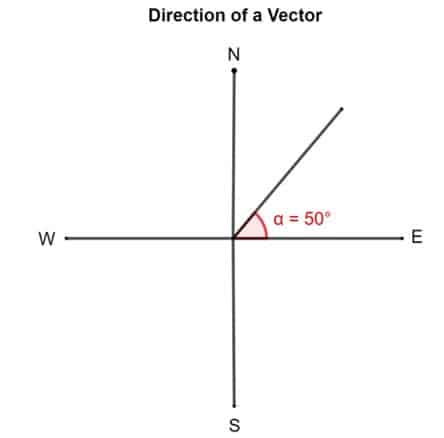
Let's see this vector diagram. If a vector is said to have a direction of 50°. The trick to figuring it out is to pivot down the tail of the vector aligned with the e or the x-axis. At present rotate the vector 50° counterclockwise most its tail.

Now take another example. Suppose a vector has a direction of 200°. This means the vector'south tail is pinned down at the E and is then rotated 200° about counterclockwise.

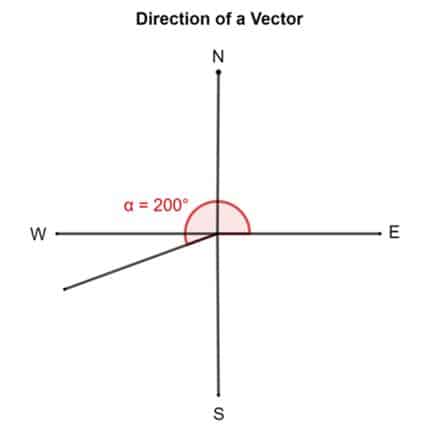
Similarly, a Rectangular coordinate system can also be used. In that instance, the angle volition be calculated from the positive 10-axis.

Now, allow's consider some examples to sympathise this concept ameliorate.

Example i

Draw a vector 30° Northward of Westward.

Solution

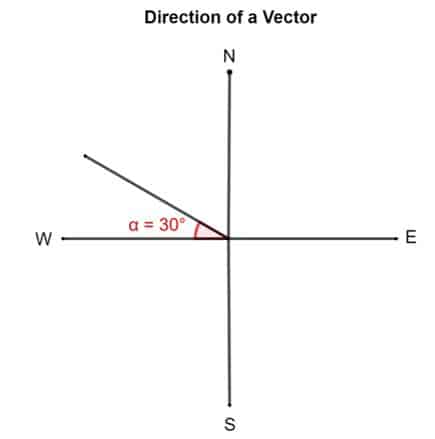
Example 2

Draw a vector with direction 60° Due east of North.

Solution

How To Notice The Direction Of A Vector?

The direction of a vector is determined by the bending it makes with the horizontal line.

In that location are 2 methods of finding the direction of a vector:

Graphical Method
Using Inverse Tangent Formula

Graphical Method

The graphical method, as the proper name suggests, requires you to draw the vector graphically and and then calculate the angle. The steps for the graphical method are as follows:

Draw the private vectors with their tails at origin and according to their angles.
Using the head-to-tail dominion, add together the vectors.
The resultant vector R is directed from the tail of the first vector A to the head of the second vector B .
The magnitude and direction of the vector are so determined by using the ruler and protractor. The length of the resultant vector R will give it magnitude.
For direction, draw a line parallel to the x-centrality passing through the starting point of the resultant vector R . Mensurate the angle between the horizontal line and the resultant.

However, hither is the problem: This method is merely for basic agreement. It gets complicated if you have to add together multiple vectors and does not always give the most accurate result. At that place is always a adventure of human error. Therefore, we accept the second method:

The Inverse Tangent Formula

We use the changed tangent office to find the angle it makes with the horizontal line .

This is possible if you have the initial and concluding coordinate points of a vector in a plane. It is given by:

θ = tan-1 (y/ten)

Case iii

A vector is directed from origin to the (3,five). Determine its management.

Solution

Here we can run across that,

a = x = 3

b = y = 5

θ = tan-1 (a/b)

θ = tan-1 (iii/5)

θ = xxx.9°

The vector is directed at thirty.nine° from the x-axis.

At present, consider a example where the tail is not located at the origin, only rather the vector is placed somewhere else in the plane. In this instance, the formula is modified as follows:

Past Pythagorean property, nosotros know:

tanθ = Δy/Δx

tanθ = (y2 – y1)/(x2 – x1)

θ = tan-1 (y2 – y1)/(x2 – x1)

So, the formula is modified as:

θ = tan-1 (y1 – y0)/(x1 – x0)

The angle given by this is from the horizontal line, running parallel to the ten-centrality.

Let's solve some examples to empathise this concept.

Example four

Discover the management of the vector located from A(2,1) to B(half-dozen,9)

Δx = x1 – x0 = vi -ii = iv

Δy = y1 – y0 = 9 -1 = eight

Solution

Using formula:

θ = tan-ane (y1 – y0)/(x1 – x0)

θ = tan-one (8/four)

θ = 63.4°

The Conventions For The Direction Of A Vector

Let's move on to a much tougher case.

We have seen that in the above example, the vector lies in the First Quadrant. Let's see how information technology works for the rest of the Quadrants. This can be adamant by the signs of the vector'south coordinates, which determine the quadrant in which the angle lies.

For this, certain conventions should be followed:

If both the coordinates are positive, and so the angle exists in the first quadrant and is considered as the standard angle. θ = Ⲫ
If the y-coordinate is positive, but the x-coordinate is negative, then the bending exists in the second quadrant so the standard bending is: θ = 180 + Ⲫ
If both the coordinates are negative, and then the bending exists in the 3rd quadrant then the standard angle is: θ = 270 + Ⲫ
If the ten-coordinate is positive, but the y-coordinate is negative, and then the standard angle is: θ = 360 + Ⲫ.

Permit's under this with the help of examples.

Example 5

Observe the direction of a vector directed from origin to the coordinates (6, -vii).

Solution

We will take help from the inverse tangent formula:

θ = tan-ane (-7/6)

θ = -49.23°

Here we tin can see from the coordinates of the vector that information technology was lying in Quadrant Iv.

Now, here is the deal:

The formula gives the shortest bending from either the positive or negative ten-centrality. The convention is to represent the bending with a positive sign from the positive x-axis. For this, we subtract from 360 ° to the obtained angle.

θ' = -49.23 + 360

θ = 310.77°

Case 6

Notice the management of the vector (-iv,3).

Solution

By looking at the coordinates, we know that the vector lies in Quadrant 2:

θ = tan-one (3/-4)

θ = -36.87°

This is the angle from the negative x-axis. Now, to go the positive respond, and calculated from the positive x-centrality counterclockwise:

θ = -36.87 + 180

θ = 143.13°

from the positive 10-axis in a counter-clockwise management.

For Finding The Direction Of The Resultant Vector

Moving on, let's meet how we tin find the management of the resultant of ii or more vectors.

As you know, to calculate the resultant vector of two or more individual vectors, we detect their respective rectangular coordinates first. Next, we add the x-component and y-component of the two vectors. The resultant ten-component and y component are, in fact, the components of the resultant vector.

Following are the pace to calculate the management of a resultant of two or more vectors:

Permit'south say y'all have vectors A and B, and yous want to discover their resultant and direction.

Deliquesce both vectors into their rectangular components.
Nosotros know, R = A + B. Similarly, Rₓ = Aₓ + Bₓ and R𝚢 = A𝚢 + B𝚢
Now using the inverse tangent belongings, replace x and y with x, y-components of the resultant, i.eastward., =ta n -1 (Ry/Rx)
Determine the quadrant of the resultant and modify theta according to it.

Practice Problems

Detect the direction of a vector whose initial and last points are (5, ii) and (four, iii), respectively.
Find the direction of a vector whose initial and final points are (ii, 3) and (5, 8), respectively.
A vector is directed from the origin to (7, 4). Find its direction.
Find the management of a vector whose coordinates are (-7, -5).
Find the direction of a vector whose coordinates are (1, -1).

Answers

-45° or 135°
59°
29.74°
234°
-45° or 135°

All the vector diagrams are constructed by using GeoGebra.

Previous Lesson | Principal Page | Adjacent Lesson